|

Posted on:
29 Sep 2013
|
It is often seen that model designers insist on eliminating the extensive variables from their model equations. The main reason that is brought up for this preference to write a model that does not involve the extensive variables is that often only the evolution of the application variables (e.g. intensive or geometrical variables) is of interest.
Also, the transfer laws and kinetic laws are usually given in terms of intensive state variables. Therefore most model designers think they must transform the accumulation terms of the (differential) balance equations and perform a so-called state variable transformation.
In most textbooks that cover modelling these transformations are also performed, often even without mentioning why. But are these, often cumbersome, state variable transformations necessary to solve the considered problems?
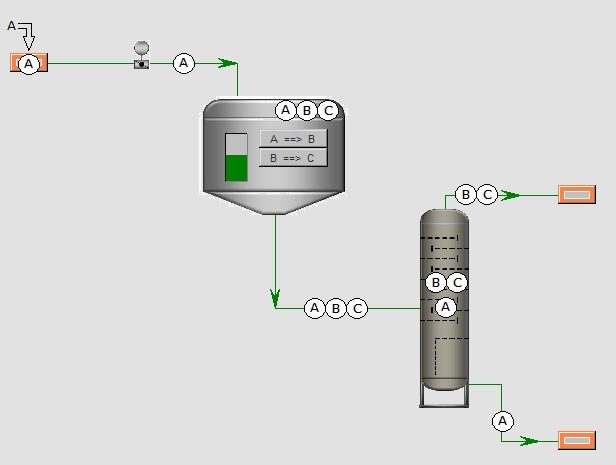
 Above you see a simple example transformation that is often used, when someone would be interested in the dynamic response of the level of a tank.
Above you see a simple example transformation that is often used, when someone would be interested in the dynamic response of the level of a tank.
An even more common transformation (which most model designers often do not even realise!), is the transformation of an Energy Balance (via the Enthalpy Balance) into an equation that represents the dynamic response of the Temperature of a system.
So, usually a modified version of this basic energy balance is employed for modelling a process component. This modified version is derived from the basic energy balance through several simplifications and assumptions.
Caution should be taken, though, when you use derived energy models, because they are often incorrect or used incorrectly. You could easily introduce faults when you are adapting or further simplifying a derived model, because of lack of knowledge about previous assumptions and derivation steps. Knowledge about the common assumptions and the derivation steps is thus essential for the correct use of the different simplified energy models.
In most cases, the transformations are not necessary. There are several reasons to consider the differential algebraic equations (DAEs) directly, rather than to try to rewrite them as a set of ordinary differential equations (ODEs):
First, when modelling physical processes, the model takes the form of a DAE, depicting a collection of relationships between variables of interest and some of their derivatives. These relationships may be generated by a modelling program (such as Mobatec Modeller). In that case, or in the case of highly nonlinear models, it may be time consuming or even impossible to obtain an explicit model.
Computational causality is, quite obviously, not a physical phenomenon, but a numerical artefact. Take, for example, the ideal gas law:
This is a static relation, which holds for any ideal gas. This equation does not describe a cause-and-effect relation. The law is completely impartial with respect to the question whether at constant temperature and constant molar mass a rise in pressure causes the volume of the gas to decrease or whether a decrease in volume causes the pressure to rise. For a solving program, however, it does matter whether the volume or the pressure is calculated from this equation.
It is rather inconvenient that a model designer must determine the correct computational causality of all the algebraic equations that belong to each modelling object, given a particular use of the model (simulation, design, etc.). It is much easier if the equations could just be described in terms of their physical relevance and that a computer program automatically determines the desired causality of each equation and solves each of the equations for the desired variable (either numerically or by means of symbolic manipulation).
Also, reformulation of the model equations tends to reduce the expressiveness.
Furthermore, if the original DAE can be solved directly it becomes easier to interface modelling software directly with design software.
Finally, reformulation slows down the development of complex process models, since it must be repeated each time the model is altered, and therefore it is easier to solve the DAE directly.
These advantages enable researchers to focus their attention on the physical problem of interest. There are also numerical reasons for considering DAEs. The change to explicit form, even if possible, can destroy sparsity and prevent the exploitation of system structure.
Small advantages of transforming the model to ODE form can be that for (very) small systems an analytical solution is available and that sometimes less information of physical properties is needed when substitutions are being made (sometimes, some of the parameters can be removed from the system equations when substitutions are made).
Another advantage could be that, by doing substitutions, some primary state variables are removed from the model description which could take the code faster, because less variables have to be solved.
In general, though, these advantages do not outweigh the disadvantages.
If one does want to perform substitutions, it is recommended that these are done at the very end of the model development and not, as is generally seen, as soon as possible. Postponing the substitutions as long as possible gives a much better insight in the model structure during model development.
I am very interested in your view on this subject:
“Are you using substitutions in your dynamic models? Were you aware of the assumptions that are made by applying substitutions?”
I invite to post your comments, insights and/or suggestions in the comment box below.
To your success!
Mathieu.
Also, the transfer laws and kinetic laws are usually given in terms of intensive state variables. Therefore most model designers think they must transform the accumulation terms of the (differential) balance equations and perform a so-called state variable transformation.
In most textbooks that cover modelling these transformations are also performed, often even without mentioning why. But are these, often cumbersome, state variable transformations necessary to solve the considered problems?

An even more common transformation (which most model designers often do not even realise!), is the transformation of an Energy Balance (via the Enthalpy Balance) into an equation that represents the dynamic response of the Temperature of a system.
So, usually a modified version of this basic energy balance is employed for modelling a process component. This modified version is derived from the basic energy balance through several simplifications and assumptions.
Caution should be taken, though, when you use derived energy models, because they are often incorrect or used incorrectly. You could easily introduce faults when you are adapting or further simplifying a derived model, because of lack of knowledge about previous assumptions and derivation steps. Knowledge about the common assumptions and the derivation steps is thus essential for the correct use of the different simplified energy models.
In most cases, the transformations are not necessary. There are several reasons to consider the differential algebraic equations (DAEs) directly, rather than to try to rewrite them as a set of ordinary differential equations (ODEs):
First, when modelling physical processes, the model takes the form of a DAE, depicting a collection of relationships between variables of interest and some of their derivatives. These relationships may be generated by a modelling program (such as Mobatec Modeller). In that case, or in the case of highly nonlinear models, it may be time consuming or even impossible to obtain an explicit model.
Computational causality is, quite obviously, not a physical phenomenon, but a numerical artefact. Take, for example, the ideal gas law:
pV = nRT
This is a static relation, which holds for any ideal gas. This equation does not describe a cause-and-effect relation. The law is completely impartial with respect to the question whether at constant temperature and constant molar mass a rise in pressure causes the volume of the gas to decrease or whether a decrease in volume causes the pressure to rise. For a solving program, however, it does matter whether the volume or the pressure is calculated from this equation.
It is rather inconvenient that a model designer must determine the correct computational causality of all the algebraic equations that belong to each modelling object, given a particular use of the model (simulation, design, etc.). It is much easier if the equations could just be described in terms of their physical relevance and that a computer program automatically determines the desired causality of each equation and solves each of the equations for the desired variable (either numerically or by means of symbolic manipulation).
Also, reformulation of the model equations tends to reduce the expressiveness.
Furthermore, if the original DAE can be solved directly it becomes easier to interface modelling software directly with design software.
Finally, reformulation slows down the development of complex process models, since it must be repeated each time the model is altered, and therefore it is easier to solve the DAE directly.
These advantages enable researchers to focus their attention on the physical problem of interest. There are also numerical reasons for considering DAEs. The change to explicit form, even if possible, can destroy sparsity and prevent the exploitation of system structure.
Small advantages of transforming the model to ODE form can be that for (very) small systems an analytical solution is available and that sometimes less information of physical properties is needed when substitutions are being made (sometimes, some of the parameters can be removed from the system equations when substitutions are made).
Another advantage could be that, by doing substitutions, some primary state variables are removed from the model description which could take the code faster, because less variables have to be solved.
In general, though, these advantages do not outweigh the disadvantages.
If one does want to perform substitutions, it is recommended that these are done at the very end of the model development and not, as is generally seen, as soon as possible. Postponing the substitutions as long as possible gives a much better insight in the model structure during model development.
I am very interested in your view on this subject:
“Are you using substitutions in your dynamic models? Were you aware of the assumptions that are made by applying substitutions?”
I invite to post your comments, insights and/or suggestions in the comment box below.
To your success!
Mathieu.











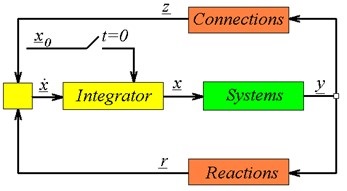
 When a dynamic process model is formulated and proper initial conditions have been defined, then the information flow of a simulation can be depicted as in the above figure. Starting from the initial conditions x0, the secondary state variables y of all the systems can be calculated (via the System Equations y=f(x)). Subsequently, the flow rates z of all the defined connections and the reaction rates r of all the defined reactions can be calculated (z = f(yor, ytar); r = f(ysys)). These rates are the inputs of the balance equations, so now the integrator can compute values for the primary state variables x on the next time step. With these variables, the secondary state y can be calculated again and the loop continues until the defined end time is reached.
When a dynamic process model is formulated and proper initial conditions have been defined, then the information flow of a simulation can be depicted as in the above figure. Starting from the initial conditions x0, the secondary state variables y of all the systems can be calculated (via the System Equations y=f(x)). Subsequently, the flow rates z of all the defined connections and the reaction rates r of all the defined reactions can be calculated (z = f(yor, ytar); r = f(ysys)). These rates are the inputs of the balance equations, so now the integrator can compute values for the primary state variables x on the next time step. With these variables, the secondary state y can be calculated again and the loop continues until the defined end time is reached.