
|

Posted on:
30 Mar 2014
|
Last month several groups of students of the “Hogeschool Utrecht” (at the faculty of Industrial Automation) finished a very educational 4 month project in which they had to design, control and simulate a part of an industrial process.
In this blog post I will discuss this project shortly and talk about some of the challenges these young students had to cope with. They managed to turn this quite demanding project into a successful, stimulating experience and I am very proud of what they have accomplished in such a short period of time.
“Is it possible to let students make a dynamic simulation of a glycol dehydration unit (used to remove water from natural gas) with the use of Mobatec Modeller? And can this ‘virtual plant’ be controlled with a real hardware PLC (also completely configured by a group of students)?”
The concepts and ideas behind Mobatec Modeller were completely new for the students, so they had quite a challenging task at hand.
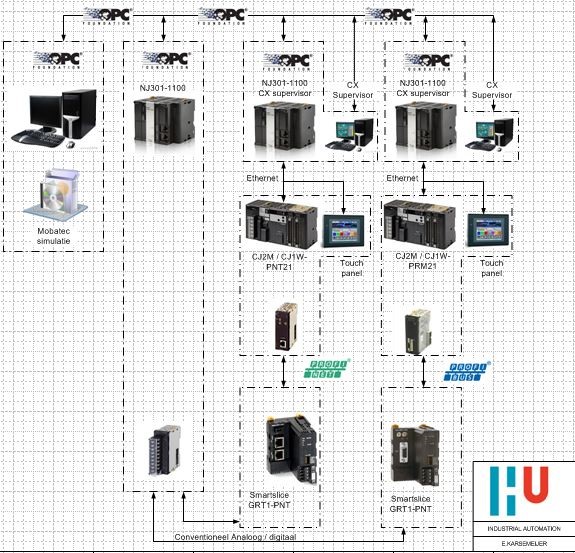
The PLC’s were to be connected to the simulation-PLC in several ways:
To build the model we provided the students with some basic (partially predefined) building blocks, since they had no background in Chemical Engineering. They had to refine and connect the building blocks and to tune the parameters to get trustworthy results. Especially the latter part, the tuning, can be quite time consuming for dynamic process models. Even more so if you do not have much experience in this field.
Obviously, since dynamic modelling was completely new for these students, some communication with Mobatec engineers was needed in order to get a good model. This interaction was kept to a minimum, however, and I was very pleased to learn how much these students were able to do themselves. Setting up and configuring the OPC connection, for example, didn’t require any interaction with us. They did this all by themselves, which is, of course, a positive outcome for both the students and Mobatec.
 Do you have any ideas or suggestions to make dynamic simulation a good learning tool for students? Or do you have other comments related to this topic?
Do you have any ideas or suggestions to make dynamic simulation a good learning tool for students? Or do you have other comments related to this topic?
Please feel free to post your experiences, insights and/or suggestions in the comment box below, such that we can all learn something from it.
To your success!
Mathieu.
———————————————–
In this blog post I will discuss this project shortly and talk about some of the challenges these young students had to cope with. They managed to turn this quite demanding project into a successful, stimulating experience and I am very proud of what they have accomplished in such a short period of time.
Project Goal
The project was used as a sort of test case, since it was the first time our modelling tool was being used by a group of students that had no background in Chemical Engineering. The main questions to be answered by the project was:“Is it possible to let students make a dynamic simulation of a glycol dehydration unit (used to remove water from natural gas) with the use of Mobatec Modeller? And can this ‘virtual plant’ be controlled with a real hardware PLC (also completely configured by a group of students)?”
The concepts and ideas behind Mobatec Modeller were completely new for the students, so they had quite a challenging task at hand.
Short Process Description
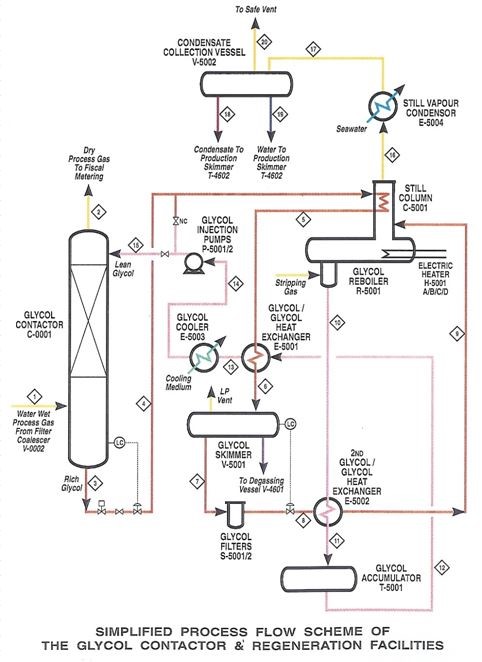
After retrieving natural gas from a well or reservoir, it still contains a substantial amount of water (liquid as well as vapor) and also some liquid carbohydrates (so-called condensates). This gas is often called wet gas and can cause several problems for downstream processes and equipment. So, before the natural gas is ready to be transported, water and condensates are removed from the gas in several steps. The Glycol Contactor is one of those steps. Glycol is a hygroscopic liquid which can easily absorb water vapor from a wet gas stream. So, by bringing the wet natural gas into contact with liquid glycol in a column, the last residues of water can be removed from the gas stream. Heating the glycol-water mixture in a Glycol Reboiler, will remove the absorbed water (by evaporation), such that the glycol can be regenerated and recycled. The picture below shows a simplified process flow scheme of the glycol contactor and regeneration facilities.
Hardware and Software Configuration
Since it was not possible for the students to realize a control setup on a real glycol dehydration unit (because such a unit was simply not available), one group of students was asked to make a real-time simulation of the process with Mobatec Modeller. Another group of students had the task to configure a real hardware PLC (Programmable Logic Controller) and configure an HMI (Human Machine Interface) and SCADA (Supervisory Control And Data Acquisition) with the available hardware and software. The simulation model should communicate via an OPC connection with a simulation-PLC.The PLC’s were to be connected to the simulation-PLC in several ways:
- Via OPC (OLE for Process Control, OLE = Object Linking and Embedding)
- Direct via analog and digital IO-signals
- Via a Fieldbus and a remote IO-station with analog and digital IO-signals

The Assignment
The project was distributed amongst six groups, two of which was responsible for the simulation. The other four groups had to design a control (with slightly different specifications) for the system.- The hardware and software configuration were thought out in big lines, but had to be designed and realized in detail by the different teams.
- The interface between the different systems, functional as well as technical, had to be determined by the teams themselves.
- The simulation of the process, including the assumptions and simplifications, had to be setup from scratch (using some building blocks). The simulation should have the option to create scenarios and “introduce errors”, such that the developed control strategies could be properly tested.
- Process conditions (under normal operation), process configuration details, battery limit (i.e. boundary) conditions and other relevant data were provided to the students, in order for them to make a realistic dynamic simulation model.
- The functional specification of the control system had to be designed by the teams.
The Modelling Effort
As a starting point for the modelling, the students had several P&ID’s (Piping and Instrumentation Diagrams) a PFD (Process Flow Diagram). The tags that were used in the P&ID’s were also used as names in the modelling environment, such that the coupling to the control PLC would be an easy task.To build the model we provided the students with some basic (partially predefined) building blocks, since they had no background in Chemical Engineering. They had to refine and connect the building blocks and to tune the parameters to get trustworthy results. Especially the latter part, the tuning, can be quite time consuming for dynamic process models. Even more so if you do not have much experience in this field.
Obviously, since dynamic modelling was completely new for these students, some communication with Mobatec engineers was needed in order to get a good model. This interaction was kept to a minimum, however, and I was very pleased to learn how much these students were able to do themselves. Setting up and configuring the OPC connection, for example, didn’t require any interaction with us. They did this all by themselves, which is, of course, a positive outcome for both the students and Mobatec.

Please feel free to post your experiences, insights and/or suggestions in the comment box below, such that we can all learn something from it.
To your success!
Mathieu.
———————————————–















 When a dynamic process model is formulated and proper initial conditions have been defined, then the information flow of a simulation can be depicted as in the above figure. Starting from the initial conditions x0, the secondary state variables y of all the systems can be calculated (via the System Equations y=f(x)). Subsequently, the flow rates z of all the defined connections and the reaction rates r of all the defined reactions can be calculated (z = f(yor, ytar); r = f(ysys)). These rates are the inputs of the balance equations, so now the integrator can compute values for the primary state variables x on the next time step. With these variables, the secondary state y can be calculated again and the loop continues until the defined end time is reached.
When a dynamic process model is formulated and proper initial conditions have been defined, then the information flow of a simulation can be depicted as in the above figure. Starting from the initial conditions x0, the secondary state variables y of all the systems can be calculated (via the System Equations y=f(x)). Subsequently, the flow rates z of all the defined connections and the reaction rates r of all the defined reactions can be calculated (z = f(yor, ytar); r = f(ysys)). These rates are the inputs of the balance equations, so now the integrator can compute values for the primary state variables x on the next time step. With these variables, the secondary state y can be calculated again and the loop continues until the defined end time is reached.