|
Posted on:
30 Nov 2013
|
Process systems engineering spans the range between process design, operations and control. Whilst experiments are essential, modelling is one of the most important activities in process engineering, since it provides insight into the behaviour of the process(es) being studied.
In previous blogs we have been discussing particular uses of models and ways to setup consistent process models. But what kind of problems can, in general, be solved by mathematical models in Process Systems Engineering?
Model :: A realisation of the modelled system, simulating the behaviour of the modelled system.
Data :: Instantiated variables of the model. May be parameters that were defined or time records of input or output data obtained from an actual plant, marketing data etc.
Criterion :: An objective function that provides a measure and which, for example, is optimised giving meaning to the term best in a set of choices.
The particular nature of the problem then depends on which of these components is known and which is to be identified. Each type of problem is associated with a name which changes from discipline to discipline. The choice of the names listed below was motivated by the relative spread of the respective term in the communities. The following principle problems are defined:
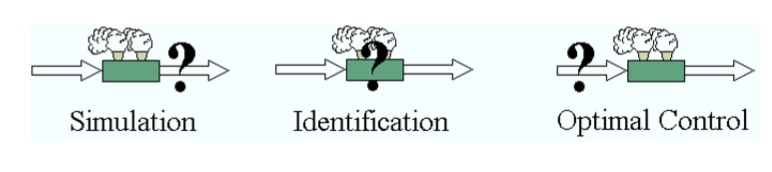Simulation: Given model, given input data and given parameters find the output of the process.
Identification: Given model structure, sometimes several structures, given process input and output data, and a given criterion, find the best structure and the parameters for the parameterised model, where best is measured with the criterion.
Optimal Control: Given a plant model, a criterion associated with process input and process output, and the process characteristics, find the best input subject to the criterion.
The definition of simulation is straightforward. (It’s the core business of Mobatec 😉 ).
The task of identification though is not, in that it includes finding structure as well as parameters of a model. This in turn implies that many tasks match this description, such as process design and synthesis, controller design and synthesis, parameter identification, system identification, controller tuning and others fit this definition.
The definition of the optimal control task is also wider than one usually would project. Namely process scheduling and planning are part of this definition as well as the design of a shut-down sequence in a sequential control problem, to mention a few non-traditional members of this class.
In all three classes a model is involved. In this discussion parameterised input/output mapping are used because they are usually the type of model capturing the behaviour of a given system in the most condensed form. Though in each case it is solved for a different set of its components. In the case of the simulation, the outputs are being computed, in the case of the identification task, the best parameters are found and in the case of optimal control, the best input record is being determined.
In order to solve a problem, the model must be supplemented with a set of definitions, which, in combination with the model, define a mathematical problem that can be solved by a particular mathematical method. These definitions are instantiations of variables that assign known quantities to variables or functions of know quantities, where the functions may be arbitrarily nested. On this highest level, process engineering problem solving has four principle components:
1. Formulation of a model;
2. Problem specification;
3. Problem solution method;
4. Problem analysis.
Several blogs have already been devoted to model formulation, but it never hurts to rephrase and repeat a bit 😉
Models take a central position in all process engineering tasks as they replace the process for the analysis. They represent an abstraction of the process, though not a complete reproduction. Models make it possible to study the behaviour of a process within the domain of common characteristics of the model and the modelled process without affecting the original process. It is thus the common part, the homomorphism or the analogy between the process and model and sometimes also the homomorphism between the different relations (= theories) mapping the process into different models that are of interest. The mapping of the process into a model does not only depend on the chosen theory, but also on the conditions under which the process is being viewed. The mapped characteristics vary thus not only with the applied theory but also with the conditions.
Different tasks focus on different characteristics and require different levels of information about these characteristics. For example control would usually be achievable with very simple dynamic models, whilst the design of a reactor often requires very detailed information about this particular part of the process. The result is not a single, all-encompassing model but a whole family of models. In fact, there is no such thing as a unique and complete model, certainly not from the philosophical point of view nor from a practical, as it simply reflects the unavoidable inability to accumulate complete knowledge about the complex behaviour of a real-world system. More practically and pragmatically a process is viewed as the representation of the essential aspects of a system, namely as an object, which represents the process in a form useable for the defined task. Caution is advised, though, as the term essential is subjective and may vary a great deal with people and application.
The term multi-faceted modelling has been coined reflecting the fact that one deals in general with a whole family of models rather than with a single model. Whilst certainly the above motivation is mainly responsible for the multi-faceted approach, solution methods also have use for a family of models as they can benefit from increasing the level of details in the model as the solution converges. An integrated environment must support multi-faceted modelling, that is mapping of the process into various process models, each reflecting different characteristics or the same characteristics though with different degree of sophistication and consequent information contents.
In the next blog post we will zoom into the assumptions that are made when making a model and the implication these assumptions can have on the end result.
To your success!
Mathieu.
———————————————–
In previous blogs we have been discussing particular uses of models and ways to setup consistent process models. But what kind of problems can, in general, be solved by mathematical models in Process Systems Engineering?
Three Principal Problems
The first step in identifying the various characteristic steps of Process Systems Engineering problem solving is to identify a minimal set of generic problems that are being solved. Most problems in this area have three major components, which are:Model :: A realisation of the modelled system, simulating the behaviour of the modelled system.
Data :: Instantiated variables of the model. May be parameters that were defined or time records of input or output data obtained from an actual plant, marketing data etc.
Criterion :: An objective function that provides a measure and which, for example, is optimised giving meaning to the term best in a set of choices.
The particular nature of the problem then depends on which of these components is known and which is to be identified. Each type of problem is associated with a name which changes from discipline to discipline. The choice of the names listed below was motivated by the relative spread of the respective term in the communities. The following principle problems are defined:
Identification: Given model structure, sometimes several structures, given process input and output data, and a given criterion, find the best structure and the parameters for the parameterised model, where best is measured with the criterion.
Optimal Control: Given a plant model, a criterion associated with process input and process output, and the process characteristics, find the best input subject to the criterion.
The definition of simulation is straightforward. (It’s the core business of Mobatec 😉 ).
The task of identification though is not, in that it includes finding structure as well as parameters of a model. This in turn implies that many tasks match this description, such as process design and synthesis, controller design and synthesis, parameter identification, system identification, controller tuning and others fit this definition.
The definition of the optimal control task is also wider than one usually would project. Namely process scheduling and planning are part of this definition as well as the design of a shut-down sequence in a sequential control problem, to mention a few non-traditional members of this class.
In all three classes a model is involved. In this discussion parameterised input/output mapping are used because they are usually the type of model capturing the behaviour of a given system in the most condensed form. Though in each case it is solved for a different set of its components. In the case of the simulation, the outputs are being computed, in the case of the identification task, the best parameters are found and in the case of optimal control, the best input record is being determined.
In order to solve a problem, the model must be supplemented with a set of definitions, which, in combination with the model, define a mathematical problem that can be solved by a particular mathematical method. These definitions are instantiations of variables that assign known quantities to variables or functions of know quantities, where the functions may be arbitrarily nested. On this highest level, process engineering problem solving has four principle components:
1. Formulation of a model;
2. Problem specification;
3. Problem solution method;
4. Problem analysis.
Several blogs have already been devoted to model formulation, but it never hurts to rephrase and repeat a bit 😉
Models take a central position in all process engineering tasks as they replace the process for the analysis. They represent an abstraction of the process, though not a complete reproduction. Models make it possible to study the behaviour of a process within the domain of common characteristics of the model and the modelled process without affecting the original process. It is thus the common part, the homomorphism or the analogy between the process and model and sometimes also the homomorphism between the different relations (= theories) mapping the process into different models that are of interest. The mapping of the process into a model does not only depend on the chosen theory, but also on the conditions under which the process is being viewed. The mapped characteristics vary thus not only with the applied theory but also with the conditions.
Different tasks focus on different characteristics and require different levels of information about these characteristics. For example control would usually be achievable with very simple dynamic models, whilst the design of a reactor often requires very detailed information about this particular part of the process. The result is not a single, all-encompassing model but a whole family of models. In fact, there is no such thing as a unique and complete model, certainly not from the philosophical point of view nor from a practical, as it simply reflects the unavoidable inability to accumulate complete knowledge about the complex behaviour of a real-world system. More practically and pragmatically a process is viewed as the representation of the essential aspects of a system, namely as an object, which represents the process in a form useable for the defined task. Caution is advised, though, as the term essential is subjective and may vary a great deal with people and application.
The term multi-faceted modelling has been coined reflecting the fact that one deals in general with a whole family of models rather than with a single model. Whilst certainly the above motivation is mainly responsible for the multi-faceted approach, solution methods also have use for a family of models as they can benefit from increasing the level of details in the model as the solution converges. An integrated environment must support multi-faceted modelling, that is mapping of the process into various process models, each reflecting different characteristics or the same characteristics though with different degree of sophistication and consequent information contents.
In the next blog post we will zoom into the assumptions that are made when making a model and the implication these assumptions can have on the end result.
To your success!
Mathieu.
———————————————–
