|
Posted on:
31 Aug 2014
|
While I was reading back through an earlier blog post on automatic component distribution, I noticed the following sentence: “To enhance the definition of the species topology, permeability and directionality are introduced as properties of mass connections. They constrain the mass exchange between systems by making the species transfer respectively selective or uni-directional.”
I realised it may not be entirely clear what is meant with the terms “permeability” and “directionality”, so I decided to spend some more lines on that:
The modelling methodology implemented in Mobatec Modeller makes use of several topologies, the Physical Topology, Species Topology and Equation Topology.
The idea of the construction of the species topology is to facilitate the definition and identification of species and reactions occurring in various parts of the processing plant. The species topology defines which species are present in which part of the process and thus defines the basics of the chemistry/biology of a processing plant model. This enables the generation of the relevant balances of extensive quantities for the systems.
The species topology is superimposed on the physical topology. Its construction efficiently aids the model designer in the definition of the chemistry/biology of the processing plant because it generates knowledge about which species are present in every system in a physical topology and about which reactions occur in every reactive system.
It should be noted that at this stage of the model definition process the quantities of the species in the systems are of no relevance. The association of a certain species with a certain system only implies that this system has a capacity for this particular species. If, for example, a system Σ is associated with only one species, S, then this implies that species S is the only species that can be present in system Σ. It does not imply that S has to be present in Σ. At certain moments or maybe all the time during an evolution/simulation of the process, species S may even be absent. At these particular moments the system has no mass, but of course still has a capacity to store the species S.
The existence of certain species and reactions in one part of the system does not imply that they are the same in all parts of the system. In principle, however, every chemical or biological species could be present in any part of the system, so one could decide not to construct the species topology and only generate a global set of species. This would mean that one defines only one set of species, which comprises all species that appear in the whole plant. Every system of the physical topology would then consist of all these species. For each species in each system the species mass balances could then be generated, which would of course result in a flood of equations. In most cases, many of these equations would be obsolete, because species are usually constrained to a group of systems and therefore do not appear in every system. The species of the fluids in the two parts of a shell and tube heat exchanger, for example, are usually not the same.
To aid in the definition of the species topology, species and reaction databases are used and three concepts are introduced, “permeability”, “directionality” and “reactions”, which support the idea of locality of chemical or biological species. These three concepts will facilitate the definition of the species topology and will be illustrated in the next sections. The permeability and directionality concepts are associated with connections and therefore with the common boundary element which the two connected systems have in common.
Permeability of Mass Connections
The permeability is defined as a property of a mass connection, which constrains the mass exchange between systems by making the species transfer selective. The mass connection is then defined as a semi-permeable thermodynamic wall. An example of a process where the permeability concept could come in handy is a simple diffusion process. The application of the selective constraint on the transportation of species can also assist in the representation of separation processes, such as ultra-filtration or reverse osmosis.
———————————————————————————-
Example: Diffusion of a Component from one Phase to Another
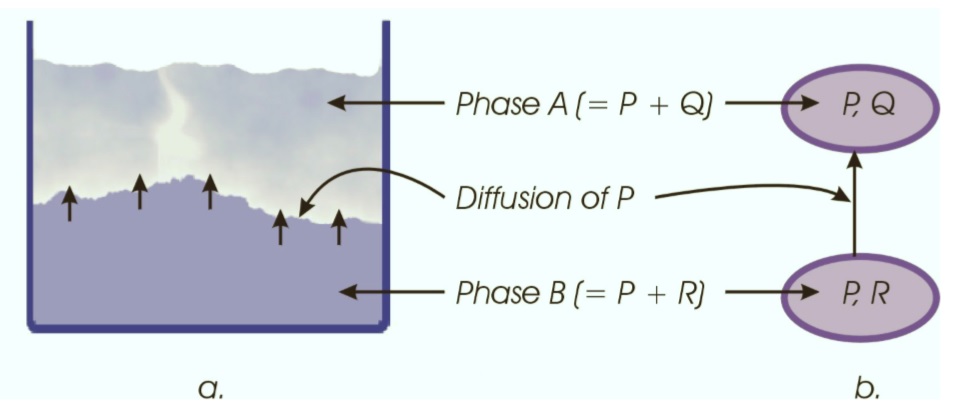Consider a tank which contains two immiscible phases A and B (figure a). Phase A consists of species P and Q. Phase B consists of species P and R. The simplest way to describe the diffusion of species P from phase A to phase B (or the other way around) is shown in figure b, which represents a physical topology of the diffusion process.
The two phases are each modelled as a simple lumped system and between the systems exists a mass connection which describes the transfer of all species between those systems. Note that the direction of the connection is only a convention, defining a reference direction for the actual stream. The actual direction of the flow depends on the driving force, which in this case would be the difference in chemical potentials of P in each phase.
To prevent the species Q and R from being transferred through the connection, the permeability concept is introduced: The connection between the two systems is defined as a semi-permeable thermodynamic wall, which is only permeable for species P. This means that only the species P will be transferred through the connection and that, consequently, the transfer terms of the other species (Q and R) will not appear in the (component) mass balances of the systems because they are not transferred.
———————————————————————————-
Note that in principle the permeability concept does not have to be limited to mass c.q. species. The concept can be readily extended to any extensive quantity. In practice, though, this is not necessary as one normally distinguishes between mass, heat, momentum and work transfer, which are all handled individually.
Directionality of Mass Connections
The concept of (uni- or bi-) directionality is also a property that is related with mass connections. The species topology, as it was described so far, allows for bi- directional flow in any mass connection. Since the flow is (normally) dependent on the state of the two connected systems, nothing can be said a priori about the direction of the actual flow.
In fact, in many situations the flow would change in the course of the time interval over which the process is being observed. Species that are not inhibited by a defined permeability may thus appear on both sides of the connection, when computing the species topology. In many applications, though, one-directional flows are assumed and thus species propagate in a constraint flow pattern across the network. This desired behaviour calls for defining two classes of mass connections, namely uni-directional and bi-directional, where the latter should be the normal case as it leaves the system unconstraint. Inversion of the flow for a uni-directional flow would have to be handled as an exception as it contradicts the validity range of the model.
Reactions
The reaction concept more or less speaks for itself. A chemical or biological reaction is a mechanism that transforms a set of species, the reactants, into a set of different species, the products. At this stage of defining the species topology it is only necessary to know which species are transformed and which species are generated in every (reactive) thermodynamic system. The properties of reactions (kinetic laws, heat of reaction, etc.) and the conditions under which the reaction may take place are introduced at a later stage.
I invite to post your experiences, insights and/or suggestions in the comment box below, such that we can all learn something from it.
To your success!
Mathieu.
———————————————–
I realised it may not be entirely clear what is meant with the terms “permeability” and “directionality”, so I decided to spend some more lines on that:
The modelling methodology implemented in Mobatec Modeller makes use of several topologies, the Physical Topology, Species Topology and Equation Topology.
The idea of the construction of the species topology is to facilitate the definition and identification of species and reactions occurring in various parts of the processing plant. The species topology defines which species are present in which part of the process and thus defines the basics of the chemistry/biology of a processing plant model. This enables the generation of the relevant balances of extensive quantities for the systems.
The species topology is superimposed on the physical topology. Its construction efficiently aids the model designer in the definition of the chemistry/biology of the processing plant because it generates knowledge about which species are present in every system in a physical topology and about which reactions occur in every reactive system.
It should be noted that at this stage of the model definition process the quantities of the species in the systems are of no relevance. The association of a certain species with a certain system only implies that this system has a capacity for this particular species. If, for example, a system Σ is associated with only one species, S, then this implies that species S is the only species that can be present in system Σ. It does not imply that S has to be present in Σ. At certain moments or maybe all the time during an evolution/simulation of the process, species S may even be absent. At these particular moments the system has no mass, but of course still has a capacity to store the species S.
The existence of certain species and reactions in one part of the system does not imply that they are the same in all parts of the system. In principle, however, every chemical or biological species could be present in any part of the system, so one could decide not to construct the species topology and only generate a global set of species. This would mean that one defines only one set of species, which comprises all species that appear in the whole plant. Every system of the physical topology would then consist of all these species. For each species in each system the species mass balances could then be generated, which would of course result in a flood of equations. In most cases, many of these equations would be obsolete, because species are usually constrained to a group of systems and therefore do not appear in every system. The species of the fluids in the two parts of a shell and tube heat exchanger, for example, are usually not the same.
To aid in the definition of the species topology, species and reaction databases are used and three concepts are introduced, “permeability”, “directionality” and “reactions”, which support the idea of locality of chemical or biological species. These three concepts will facilitate the definition of the species topology and will be illustrated in the next sections. The permeability and directionality concepts are associated with connections and therefore with the common boundary element which the two connected systems have in common.
Permeability of Mass Connections
The permeability is defined as a property of a mass connection, which constrains the mass exchange between systems by making the species transfer selective. The mass connection is then defined as a semi-permeable thermodynamic wall. An example of a process where the permeability concept could come in handy is a simple diffusion process. The application of the selective constraint on the transportation of species can also assist in the representation of separation processes, such as ultra-filtration or reverse osmosis.
———————————————————————————-
Example: Diffusion of a Component from one Phase to Another
The two phases are each modelled as a simple lumped system and between the systems exists a mass connection which describes the transfer of all species between those systems. Note that the direction of the connection is only a convention, defining a reference direction for the actual stream. The actual direction of the flow depends on the driving force, which in this case would be the difference in chemical potentials of P in each phase.
To prevent the species Q and R from being transferred through the connection, the permeability concept is introduced: The connection between the two systems is defined as a semi-permeable thermodynamic wall, which is only permeable for species P. This means that only the species P will be transferred through the connection and that, consequently, the transfer terms of the other species (Q and R) will not appear in the (component) mass balances of the systems because they are not transferred.
———————————————————————————-
Note that in principle the permeability concept does not have to be limited to mass c.q. species. The concept can be readily extended to any extensive quantity. In practice, though, this is not necessary as one normally distinguishes between mass, heat, momentum and work transfer, which are all handled individually.
Directionality of Mass Connections
The concept of (uni- or bi-) directionality is also a property that is related with mass connections. The species topology, as it was described so far, allows for bi- directional flow in any mass connection. Since the flow is (normally) dependent on the state of the two connected systems, nothing can be said a priori about the direction of the actual flow.
In fact, in many situations the flow would change in the course of the time interval over which the process is being observed. Species that are not inhibited by a defined permeability may thus appear on both sides of the connection, when computing the species topology. In many applications, though, one-directional flows are assumed and thus species propagate in a constraint flow pattern across the network. This desired behaviour calls for defining two classes of mass connections, namely uni-directional and bi-directional, where the latter should be the normal case as it leaves the system unconstraint. Inversion of the flow for a uni-directional flow would have to be handled as an exception as it contradicts the validity range of the model.
Reactions
The reaction concept more or less speaks for itself. A chemical or biological reaction is a mechanism that transforms a set of species, the reactants, into a set of different species, the products. At this stage of defining the species topology it is only necessary to know which species are transformed and which species are generated in every (reactive) thermodynamic system. The properties of reactions (kinetic laws, heat of reaction, etc.) and the conditions under which the reaction may take place are introduced at a later stage.
I invite to post your experiences, insights and/or suggestions in the comment box below, such that we can all learn something from it.
To your success!
Mathieu.
———————————————–
